How will quantum impact cryptography?

In 1965, Gordon Moore determined that the number of components on an integrated circuit doubled every year, and then refined this to doubling every two years. The prediction has since been proven fairly accurate — but this could be coming to an end, as we just can’t shrink transistors any further. The way forward, perhaps, is to move towards optical devices; these will allow us to achieve lightning-fast speeds and parallel processing that would break away from our electrical circuit constraints.  The dream in quantum is to build computers which process qubits and are basic stores of quantum information. We can then represent our binary information as one of two states of the qubit, such as the spin of an electron or the polarisation of a proton. And with this, we can add an inherent feature of quantum mechanics: the superposition of multiple states simultaneously.

A whole world built on cryptography

We depend greatly on cryptographic methods for our privacy and in the trust of the systems we connect to. Without them, we would be open to adversaries reading and changing our communications, and we would not be able to tell if we were connecting to a valid website or a fake one. At the core of this is the creation of a trusted encryption tunnel that sets up a connection between one host (a client) and another (a server). The concept of using the same key to encrypt and decrypt our data — symmetric key encryption — has been around since the 1950s and is at the core of keeping our data secure. The most widely used methods these days are AES and ChaCha20. It is thus typically symmetric key encryption which protects our data from being viewed by Eve (our adversary), and which allows for Bob and Alice to send secret messages to each other.

But, in 1976, Whitfield Diffie and Marty Hellman published a paper that changed the world of cybersecurity, and which proposed the opportunity of using two keys: a public key and a private key. The keys were interchangeable. The public key could encrypt, and the private key decrypt. Along with this, they proposed a way of creating a shared symmetric key that involved Bob and Alice sharing a public value of a secret. This is known as the Diffie-Hellman (DH) method and is at the core of many of the connections that we make to the internet. As shown in Figure 1, the method uses discrete logarithms, with a base generator of g and a large prime number of p. So, even if Eve knows g and p, she should not be able to determine Bob or Alice’s secret values. While initially implemented with discrete logs, we now implement the DH method with elliptic curves. This is known as ECDH (Elliptic Curve Diffie Hellman).

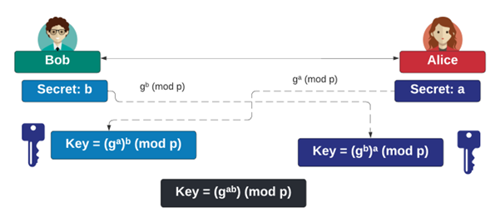
So, while Bob and Alice can generate the same symmetric key for their communications with ECDH, we now have the problem of an Eve-in-the-middle attack, where Eve can negotiate two encryption tunnels and then read the secret communications. For this, we introduce the concept of public key encryption. Rivest, Shamir and Adleman produced the RSA method, one of the first public key encryption systems, just one year after Diffie and Hellman proposed the opportunity to use public key encryption. We could now use a public key to encrypt data and a private key to decrypt it. But the methods involved in public key encryption are often much more processor intensive than symmetric key encryption, and so the data we encrypt is often small — such as encrypting encryption keys. Where public key encryption comes in most useful is in the creation of digital signatures, where Bob uses his private key to sign a hash of a message and Alice then uses his public key to verify the signature (Figure 2). The most common digital signatures are RSA, ECDSA (Elliptic Curve Digital Signature Algorithm) and EdDSA (Edwards-curve DSA).

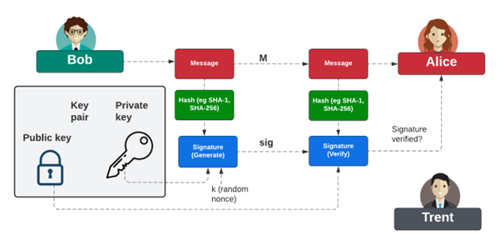
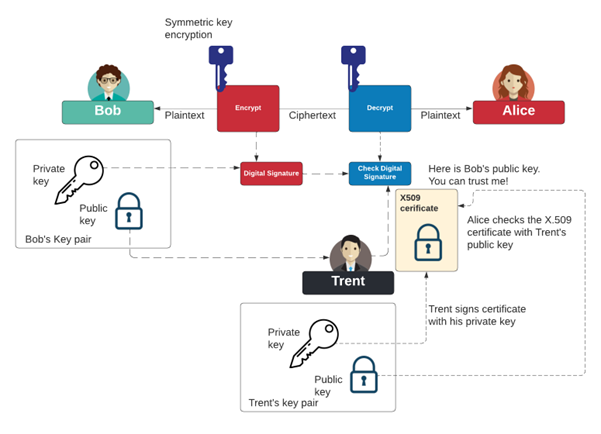
For privacy and trust on the internet, a symmetric key is then typically used to encrypt data between Bob and Alice. The key is created with ECDH, and creates trust between Bob and Alice through digital signing. For this, as illustrated in Figure 3, Bob signs the messages passed to Alice with his private key, and then Alice is passed his public key. For trust, Alice needs to know that she is receiving Bob’s actual public key, so we introduce Trent, who will sign Bob’s public key and produce a digital certificate for Alice to examine. If she trusts Trent, she will trust Bob’s public key. This infrastructure creates the PKI (Public Key Infrastructure).

Quantum cracking

The move towards quantum computers, where we’re seeing systems created with quantum circuits, has already started. This includes converting our conventional logic gates into quantum logic gates. Unfortunately, one of the things that quantum computers are good at is breaking our existing cryptography methods; for example, Peter Shor found that it was possible to factorise a modulus (N) into its prime number factors without the extensive computation of our existing methods.

For you

Be part of something bigger, join BCS, The Chartered Institute for IT.

This creates a problem, as the RSA public key encryption method relies on the difficulty of integer factorisation; it generates two prime numbers (p and q) which it then multiplies together to give a modulus (N), which is then used as the key to encrypt data. For modulus sizes of over 2,048 bits, we would have to consume the equivalent amount of energy needed to boil all the oceans on the planet to factorise it (p121). Once we factorise the modulus, it is a trivial task to then find out the private key that is associated with the modulus; and quantum computers can do this factorising much more easily.

So, unfortunately, all of the public key encryption and key exchange methods that we use on the internet will be cracked by quantum computers. Along with this, Lov Gover outlined a method of building large tables of encryption keys within a quantum computer, which causes a risk for our symmetric key and hashing methods. With this, though, there is less of a risk than the breaking of public key methods — and, in most cases, organisations simply need to move from 128-bit symmetric key and hashing towards 256-bit implementations.

NIST standardisation

Luckily, NIST started a competition to find replacements for our existing public key methods in 2016 and undertook an extensive review of the performance and security of a range of proposed methods. NIST estimated that there was a one-in-seven chance of RSA-2048 being broken by 2026, and a one-in-two chance by 2031. The methods analysed involved problems that were known to be quantum robust, including lattice methods, isogenies, multivariates and hash-based methods. The competition involved two main aspects: key encapsulation (which will replace key exchange), and digital signatures. For key encapsulation and public key encryption, NIST selected the lattice-based approach of CRYSTALS-Kyber (FIPS 203); for digital signatures, they selected the lattice-based approaches of CRYSTALS-Dilithium (FIPS 204) and FALCON, and the hash-based approach of SPHINCS+ (FIPS 205).

Lattice methods generally were the fastest of the submitted methods, and have relatively small keys. Kyber738, for example, has a public key of 1,184 bytes, a cipher of 1,088 bytes and a private key of 2,400 bytes. This can be compared with ECDH, which has a public key of just 64 bytes and a private key of 32 bytes. For signatures, with Dilithium2, we have 1,312 bytes for the public key, 2,528 bytes for the public key, and 2,420 bytes for the digital signature. This compares to just 32 bytes for the private key, 64 bytes for the public key, and 256 bytes for the digital signature for ECDSA. RSA-2048 has 256 bytes for the private key, public key and signature.

Overall, the lattice-based approaches use large lattices of points where a small amount of noise is added to the points. It is then a hard problem to find the nearest point to a point in the lattice. Unfortunately, it is not a provable hard problem, and so NIST is assessing other non-lattice methods for both key encapsulation and digital signatures. These include McElliece, HQC and BIKE for key encapsulation, and a new NIST competition for additional signatures.

Conclusions

The search for non-lattice methods continues — but one thing that is for sure is that we need to start the migration for our key exchange and digital signatures soon. It is likely, though, that this will not be a ‘big bang’ approach. In most cases, we will implement a hybrid approach, where ECDH will sit alongside Kyber in the packets exchanged, and we will be double signing with RSA, ECDSA and EdDSA alongside Dilithium signatures. At some time in the future, though, we will probably have to switch off our existing public key methods, and deprecate them from the internet.